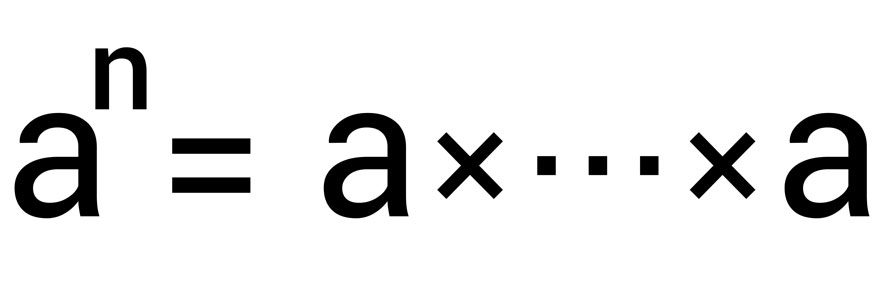Il est facile de se perdre avec les différentes règles de calcul lors de leur utilisation. Les règles de calcul sur les puissances ne manquent pas à cette confusion. Pourtant, elles sont l’une des bases des calculs en algèbre et doivent être utilisées avec automatisme. Mais quelles sont les règles de calcul à savoir sur les puissances ? Avant d’y parvenir, il est indispensable de connaître ce qu’est la puissance, quand et comment l’utiliser ?
La définition d’une puissance
Une puissance se définit comme étant le nombre de fois par lequel un nombre est multiplié par lui-même, c’est-à-dire que la valeur de la puissance correspond au nombre de fois où on écrit un chiffre ou un nombre ou bien au nombre de signes de multiplication plus un. Par exemple, 24 = 2 x 2 x 2 x 2, on voit que le chiffre 2est écrit 4 fois donc la valeur de la puissance est 4, la signe de multiplication est écrit 3 fois et on ajoute plus un et on obtient la valeur de la puissance qui est 4. De même, 2 x 2 x … x 2 (n-fois) s’écrit 2n et comporte (n-1) signe de multiplication. La puissance est à différencier de la multiplication qui peut se faire entre différents nombres.
Il est possible d’écrire une puissance de différentes manières, la plus utilisée est celle de l’exposant. La valeur de la puissance est écrite en haut à droite du nombre qui la porte, elle est de la forme : q^k avec q un nombre quelconque et k un entier, k est un exposant (ex : 3^7). Des fois, on utilise q^k pour la représenter surtout dans les calculatrices (ex :5^6). Et pour les puissances de 10, certaines calculatrices affichent « 3E+4 » ou « 3e+4 » ce qui correspond à 3×10^4.
q^k peut se lire q puissance k ou q exposant k.
Pour les puissances 2, on peut aussi dire « carré » donc q² se lit q carré. De même pour les puissances 3, on utilise « cube » donc q³ correspond à q cube. Pour plus d’information : www.accromaths.fr
Les différents exposants des puissances
– Puissance à exposant positif
Un exposant positif est un entier naturel non-nul c’est-à-dire supérieur à zéro. Donc, une puissance avec un exposant positif est un entier quelconque avec un exposant positif. Par exemple, 7² ou 4³ etc. Notez qu’un chiffre quelconque avec une puissance égale à un est égale au chiffre lui-même et 1 avec un exposant positif est toujours égale à 1 (q^1 = q et 1^n = 1).
– Puissance à exposant zéro
Ici, la valeur de la puissance est égale à zéro. Des conventions ont été adoptées pour faciliter les calculs avec les puissances zéro. L’une adopte qu’un chiffre quelconque puissance zéro est égale à un, par exemple 9^0= 1 et q^0 = 1 : c’est la convention sur les produits vides. L’autre convention est que 0^0 = 1, elle peut être utilisée pour identifier un polynôme à un cadre plus abstrait.
– Puissance à exposant négatif
L’exposant k est ici négatif donc la puissance est de la forme q^-k. Une puissance négative équivaut à l’inverse de la puissance positive c’est-à-dire que q^-k = 1/q^k. Par exemple, 9^(-3) = 1/9^3 ou 1/4^6 = 4^(-6). On peut donc avoir une puissance positive à partir d’une puissance négative en inversant la fraction. Si k=1, q^(-1) = 1/q.
Le cas particulier des puissances de 10
Les puissances de 10 permettent d’écrire de grands nombres, de petits nombres et les décimales. Donc, les puissances de 10 sont utilisées pour abréger les écritures de ces nombres. En général, elles se basent sur les écritures des nombres multiples de 10 et le nombre de zéro écrit correspond à la valeur de la puissance. Par exemple, 100 = 10^2 et 100000 = 10^5, on peut observer que dans 100 il y a deux zéros et dans 100000 il y a cinq zéros d’où la valeur des exposants. Cependant, il est possible d’utiliser les puissances de 10 pour les nombres qui ne sont pas multiples de 10 en utilisant le même principe, multiplier le reste de la division avec 10 par une puissance de 10. Par exemple, 53000 = 53 x 1000 = 53 x 10^3 ou 24200 = 242 x 10^2. Pour les petits nombres entre 0 et 1, il est plus facile de les écrire avec les puissances de 10 en multipliant le premier nombre différent de 1 par une puissance de 10. La puissance a ici un exposant négatif. Par exemple, 0.000027 = 27 x 10^(-5) et 0.0001 = 10^(-4). Pour les nombres décimaux, on déplace la virgule jusqu’au dernier chiffre non nul. Par exemple, 2,24 = 2 x 10^(-2) ou 7,5487454 = 75487454 x 10^(-7). Les puissances de 10 sont donc de la forme q x 10^k.
Les règles de calcul sur les puissances
. a^x x a^y = a^(x+y)
Ex : 2^3 x 2^5 = 2^8
. a^x / a^y = a^(x-y)
Ex : 2^5 / 2^3 = 2^2
. (a^x)^y = a^xy
Ex : (2^3)^4 = 2^12
. (a x b)^x = a^x x b^x
Ex : (3 x 7)^9 = 3^9 x 7^9
. (a / b)^x = a^x / b^x
Ex : (4 / 9)^6 = 4^6 / 9^6